HapInS Developers Blog

HapInSが提供するエンジニアリングの情報サイト

トップ > 言語処理系 > ラムダ計算第2回　引き算と割り算をしよう！

ラムダ計算第2回　引き算と割り算をしよう！

言語処理系 計算理論

こんにちは！ HapInSアドベントカレンダー2023、8日目を担当するh_shimakawaです。 今回も引き続きラムダ計算を続けていきます。

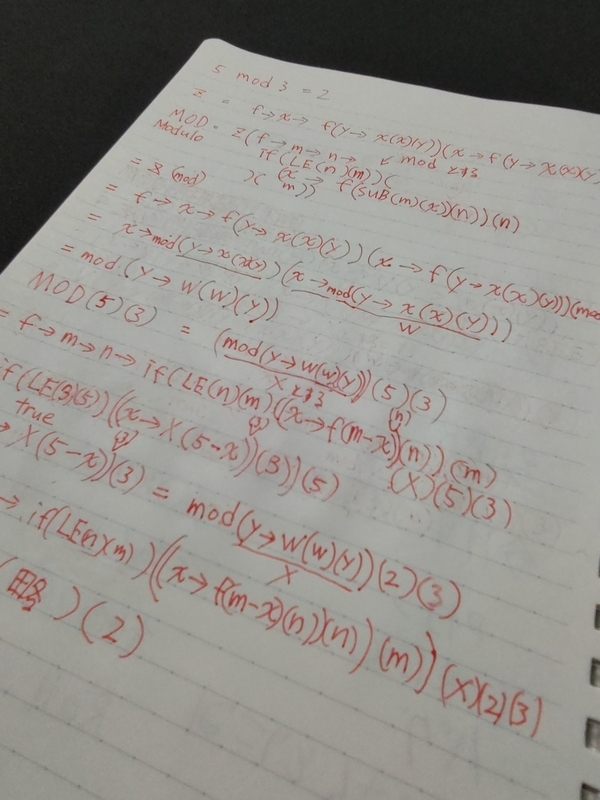
はじめに

ラムダ計算第１回記事では、真偽値と数値、たし算とかけ算を定義しました。 今回は引き算と割り算の定義を行います。

ひき算とわり算の実装には、思ったよりたくさんの準備が必要なので頑張って進めましょう。

この記事は第１回の記事を読んだ方が対象です。 まだ読んでいない方は　こちら ラムダ計算第1回: ラムダ計算を楽しもう！ - HapInS Developers Blog を先にお読みください。

難易度

Level: 第１章が分かれば多分いけます。

今回も置き去りにならないようしっかりついてきてください。

目標

この連載ではラムダ計算の機能を実装することで、ラムダ計算がチューリング完全な機能を持つことを証明します。

今回のテーマは以下の第 2 章にあたります。 たし算、わり算よりもちょっと難しいひき算、わり算に取り組みます。

  • 第 1 章 ラムダ計算の基礎と真偽値、数値とたし算、かけ算
  • 第 2 章 ひき算とわり算、コンビネータ
  • 第 3 章 リスト構造とリストの処理
  • 第 4 章 チューリングマシンの作成

用意するもの

  • 推奨: 紙とペン
  • なければ: パソコン

ひき算の作成準備

では早速始めましょう。

みなさん早速ですが 、引き算(SUB) の実装は、足し算(ADD) を参考にすればいいと思いますよね？ きっとこんなかんじですよね？

// const ADD = m => n => m(INC)(n)
const SUB = m => n => m(DEC)(n)

ではそのような DEC を考えてみましょう。 例えば DEC(TWO)だと p=>n=>p(p(n))から p の適用 を一個取れば ONE (p=>n=>p(n))ができそうですね！

皆さんできますか？ ちょっとどうやったら書けるか考えてみましょう。

ちなみに私は全然できませんでした。 DEC は簡単に見えて、実装は非常に複雑で、いくつか部品が必要になります。

PAIR と LEFT、RIGHT の実装

「PAIR の実装は第3章のリストに関連するんじゃ無いの?」と思った皆さん！ 鋭いですね！

確かに PAIR が主役になるのは次の掲載です。 ですが PAIR/LEFT/RIGHT は DEC を作る上で必要な関数なのでここで 定義します。

まず、PAIR は二つの組み(ペア)を作る関数です。 また、LEFT と RIGHT は PAIR で作った値からペアの片方を取得するために必要な関数です。

これらの関数を組み合わせることで、配列（リスト）やオブジェクトなど、複雑なデータ構造を組み立てることができます。

// 定義
const PAIR = l => r => f => f(l)(r);
const LEFT = p => p(l => r => l);
const RIGHT = p => p(l => r => r);
// 確認用コード
const create = id => name => age => PAIR(id)(PAIR(name)(age));
const getId = LEFT;
const getName = user => LEFT(RIGHT(user));
const getAge = user => RIGHT(RIGHT(user));
const user1 = create('001')('taro')('20');
console.log(getId(user1)); // 001
console.log(getName(user1)); // taro
console.log(getAge(user1)); // 20

PAIR は IF と引数の順番が違うだけの関数ですね。

そして LEFT/RIGHT はそれぞれ TRUE/FALSE に似た関数になっています。

SLIDE

先ほど定義した PAIR を使うことで、m-1とmのペアを作ることができるようになります。

SLIDE は[0,0]から始まって、[0,0]→[0,1]→[2,3]→[3,4]→[4,5]のように右から左にスライドすることで、[n-1,n]を作る関数です。

// 定義
const SLIDE = p => PAIR(RIGHT(p))(INC(RIGHT(p)));
// 確認用コード
const slide1 = SLIDE(PAIR(ZERO)(ZERO));
const slide2 = SLIDE(SLIDE(PAIR(ZERO)(ZERO)));
const slide3 = SLIDE(SLIDE(SLIDE(PAIR(ZERO)(ZERO))));
console.log(TO_INT(LEFT(slide1)), TO_INT(RIGHT(slide1))); // 0,1
console.log(TO_INT(LEFT(slide2)), TO_INT(RIGHT(slide2))); // 1,2
console.log(TO_INT(LEFT(slide3)), TO_INT(RIGHT(slide3))); // 2,3

SLIDE を n 回適用すると、[ n-1, n] のペア が取得できますね。 ただし、n=0 の時は [0,0] が返ります。（これ、重要です。）

DEC の定義

たくさんの準備が必要でしたが、これでようやく DEC を実装できます。

// 定義
const DEC = n => LEFT(n(SLIDE)(PAIR(ZERO)(ZERO)));
// 確認用コード
console.log(TO_INT(DEC(TWO))); // 1

なお、この DEC では負数を扱うことができません。 SLIDE の仕様により DEC(ZERO)は ZERO に評価されます。（これ重要です！）

ひき算

ではひき算を定義しましょう。

// 定義
const SUB = m => n => n(DEC)(m);
// 確認用コード
console.log(TO_INT(SUB(FOUR)(THREE))); // 1

長く大変な道のりでしたがようやくひき算を実装できました！ なお、DEC の仕様により、m < n のとき、DEC(m)(n)の計算結果が 0 になります。 このことは覚えていてください。（これ重要です！重要なので3回言いました！）

わり算の準備

わり算については仕様を決める必要があります。 というのも、今実装しているラムダ計算の体系には 0 と正数しか存在していません。 説明と実装の簡略化のため、計算結果も0と正数にする必要があります。 なので、10➗3🟰商3、あまり1という計算を行い、計算結果が現在の扱っている数値体系で表現できるようにします。

わり算についてもいくつかの準備が必要です。 どんな機能が必要でしょうか？

わり算の計算を Javascript で書くと以下のようになります。

const div = (m,n,count=0) => {
  if(n<=m) return div(m-n, n, count+1)
  else return count
}

この中で現在のラムダ計算の体系にないものは何でしょうか？ それはa<=bと再帰です。

LE

LE(less or equal, <=)を実装します。

a<=b は、式を変形すると a-b<=0 ですね！

さっき定義した SUB は計算結果がマイナスになるとき 0 を返すので（伏線回収）、a-bが0 になることを確認すればいいですね！

// 定義
const LE = m => n => IS_ZERO(SUB(m)(n));
// 確認用コード
console.log(IF(LE(ONE)(TWO))('yes')('no')); // yes
console.log(IF(LE(TWO)(TWO))('yes')('no')); // yes
console.log(IF(LE(TWO)(ONE))('yes')('no')); // no

さっき定義した SUB がちょうどいい感じに働いていますね。

無名再帰関数

割り算(DIV)と余り(MOD)を計算するするには繰り返し処理が必要です。 ですが、ラムダ計算には for 文や while 文のような繰り返しの制御構文がありません。

なので、繰り返しは再帰呼び出しで実現させます。

では、どうやって再起呼び出しをするのでしょうか？ 普通は再帰関数は自分自身を呼び出せばいいのですが、ラムダ計算では、再帰（関数がその関数自身を呼び出す）をさせるのに一工夫が必要です。

例えば以下のようなプログラムを考えることができます。

// 再帰の例（でもconstで名前をつけた変数DIV_TESTを使うので正しくない）
const DIV_TEST = m => n => c => IF(LE(m)(n))(c)(DIV_TEST(SUB(m))(n)(INC(c)))
// 確認用コード
console.log(TO_INT(DIV_TEST(MUL(FOUR)(FOUR))(THREE)(ZERO)))

上記は一応正しい計算結果を得ることができます。

ですが、これは繰り返しになりますが、ラムダ計算では const のように変数を定義することはできないので、これは厳密にはラムダ計算ではありません。 なので、以下で紹介するコンビネータを定義して再帰を実現する必要があります。

Z コンビネータ

これを解決できるのは、Z コンビネータと呼ばれるものです。 今回の記事では使いませんが、メジャーな再帰の実現手段なので一応紹介します。 詳しい紹介は「Z コンビネータ」で検索してみてください。

const Z = f => x => f((y) => x(x)(y))(x => f(y => x(x)(y)));

FIX コンビネータ

さて、もう少しシンプルに再帰処理を実現できる FIX 関数を紹介します。 本記事では再帰にFIX関数を採用します。

const FIX = f => f(f);

引数fを一つだけ取って、fを引数にfを呼び出しています。

でもこれだけ見てもどうやって使うのかイメージわかないと思います。

MOD(割り算の余り)の定義

では、先ほど定義したFIXを使って、繰り返し計算が必要な、割り算の"あまり"を計算するMODを定義してみましょう。 a / bのあまりを計算するには、aからbを何回も引き算して、もう引き算ができなくなった時に残った数を求めればいいので、以下のようになります。

// 定義
const MOD_LOOP = f => m => n =>
  IF(LE(n)(m))(x => f(f)(SUB(m)(n))(n)(x))(m);
const MOD = FIX(MOD_LOOP);
// 確認用コード
console.log(TO_INT(MOD(FIVE)(THREE))); // 2

計算してみましょう

MOD(FIVE)(THREE)
= FIX(MOD_LOOP)(FIVE)(THREE)
= MOD(MOD_LOOP)(FIVE)(THREE)
= (f => m => n => IF(LE(n)(m))(x => f(f)(SUB(m)(n))(n)(x))(m))
    (MOD_LOOP)(FIVE)(THREE)
= IF(LE(THREE)(FIVE))(x => MOD_LOOP(MOD_LOOP)(SUB(FIVE)(THREE))(THREE)(x))(FIVE)
= x => MOD_LOOP(MOD_LOOP)(SUB(FIVE)(THREE))(THREE)(x)
= x => MOD_LOOP(MOD_LOOP)(TWO)(THREE)(x)

計算が途中で止まって、数値ではなく、関数が返ってきましたね（数値も関数ですが・・・） これは「5割る3の余り」は、「2割る3の余り」を返す関数とみなすことができます。 でも、どうしてx => なんとか(x)のように関数で包む必要があるのでしょうか？ 実はこれは遅延評価と呼ばれるもので、実行を遅らせる効果があります。 ではなぜ評価を遅らせる必要があるのでしょうか？

それはIF(FALSE)(a)(b)のケースでもJavascriptでは引数aが評価されてしまい、 aで再帰関数の呼び出しを行なっていた場合はいつまでも再帰を繰り返して計算が終わらずStackOverFlowでプログラムが落ちてしまうからです。 これを避けるためにx => XXXX(x)のようにして実行を遅らせる必要があります。

では、これを仮にINC(MOD(FIVE)(THREE))を計算してみましょう。

INC(MOD(FIVE)(THREE))
= INC(x=>MOD(MOD)(TWO)(THREE)(x))
= (n=>p=>x=>p(n(p)(x)))(y=>MOD(MOD)(TWO)(THREE)(y)) // INC=(n=>p=>x=>x(n(p)(x)))
= p=>x=>p((y=>
    MOD(MOD)(TWO)(THREE) // この行をPとする
      (y))(p)(x))
= p=>x=>p((y=>TWO(y))(p)(x)) // PはTWOである
= p=>x=>p(TWO(p)(x)) // yにpを適用
= p=>x=>p(p(p(x)))
= THREE

P = MOD(MOD)(TWO)(THREE)
= (f => m => n =>IF(LE(n)(m))((x) => f(f)(SUB(m)(n))(n)(x))(m))
    (MOD)(TWO)(THREE)
= IF(LE(THREE)(TWO))((x) => MOD(MOD)(SUB(TWO)(THREE))(THREE)(x))(TWO)
= TWO

1 + (5➗3の余り)は1+2 = 3なので、あっていますね！

constで変数宣言しなくても問題なく再帰処理ができます。

DIVの定義

割り算の商を計算するDIVを作成します。 a % b の時、何回aからbを何回引き算できるかを数えればいいですね！

// 定義
const DIV_LOOP = f => m => n => c =>
  IF(LE(n)(m))(x => f(f)(SUB(m)(n))(n)(INC(c))(x))(c);
const DIV = m => n => FIX(DIV_LOOP)(m)(n)(ZERO);
// 確認用コード
console.log(TO_INT(DIV(SEVEN)(THREE))); //2

では実際に式を展開してみましょう。

前回と同様に遅延評価されるのでINCも使います。

INC(DIV(SEVEN)(THREE))
= INC(m=>n=>(FIX(DIV_LOOP)(m)(n)(ZERO))(SEVEN)(THREE))
= INC(FIX(DIV_LOOP)(SEVEN)(THREE)(ZERO))
= INC(DIV_LOOP(DIV_LOOP)(SEVEN)(THREE)(ZERO))
= INC((f=>m=>n=>c=>IF(LE(n)(m))(x=>f(f)(SUB(m)(n))(n)(INC(c))(x))(c))
    (DIV_LOOP)(SEVEN)(THREE)(ZERO))
= INC(IF(LE(THREE)(SEVEN))(x=>DIV_LOOP(DIV_LOOP)(SUB(SEVEN)(THREE))(THREE)(INC(ZERO))(x))(ZERO))
= INC(x=>DIV_LOOP(DIV_LOOP)(SUB(SEVEN)(THREE))(THREE)(INC(ZERO))(x))
= INC(x=>
    DIV_LOOP(DIV_LOOP)(FOUR)(THREE)(ONE)
      (x))
= INC(x=>
    DIV_LOOP(DIV_LOOP)(FOUR)(THREE)(ONE)
      (x))
= INC(x=>
    (f=>m=>n=>c=>IF(LE(n)(m))(x => f(f)(SUB(m)(n))(n)(INC(c))(x))(c))
      (DIV_LOOP)(FOUR)(THREE)(ONE)
      (x))
= INC(x=>
    (IF(LE(THREE)(FOUR))
      (y => DIV_LOOP(DIV_LOOP)(SUB(FOUR)(THREE))(THREE)(INC(c))(y))
    (ONE)
  )(x))
= INC(x=>
    (IF(LE(THREE)(FOUR))
      (y => (f=>m=>n=>c=>IF(LE(n)(m))(x => f(f)(SUB(m)(n))(n)(INC(c))(x))(c))(DIV_LOOP)(SUB(FOUR)(THREE))(THREE)(INC(c))(y))
    (ONE)
  )(x))
= INC(x=>ONE(x))
= (n=>p=>z=>z(n(p)(z)))(x=>ONE(x))
= (p=>z=>z(x=>ONE(x)(p)(z)))
= (p=>z=>z(x=>ONE(x)(p)(z)))
= (p=>z=>z(x=>(x(p))(z)))
= p=>z=>z(z(p))
= TWO

さあ展開しよう！

今回の記事で一番複雑なDIV(7/3)を展開してみましょう。

このコードを見てもほとんど意味がわかりませんが、最後の方に7と3が見えてますね。p(p(p(...(n)))の部分です。

今回で引き算、割り算、再帰（繰り返し）の実装である程度の数値計算はできるようになってきました。 感動もひとしおですね！

console.log((x=>x(n=>n+1)(0))(((m)=>(n)=>((f)=>f(f))((f)=>(m)=>(n)=>(c)=>((c)=>(x)=>(y)=>c(x)(y))(((m)=>(n)=>((n)=>n((x)=>(x)=>(y)=>y)((x)=>(y)=>x))(((m)=>(n)=>n((n)=>((p)=>p((l)=>(r)=>l))(n((p)=>((l)=>(r)=>(f)=>f(l)(r))(((p)=>p((l)=>(r)=>r))(p))(((n)=>(p)=>(x)=>p(n(p)(x)))(((p)=>p((l)=>(r)=>r))(p))))(((l)=>(r)=>(f)=>f(l)(r))((p)=>(n)=>n)((p)=>(n)=>n))))(m))(m)(n)))(n)(m))((x)=>f(f)(((m)=>(n)=>n((n)=>((p)=>p((l)=>(r)=>l))(n((p)=>((l)=>(r)=>(f)=>f(l)(r))(((p)=>p((l)=>(r)=>r))(p))(((n)=>(p)=>(x)=>p(n(p)(x)))(((p)=>p((l)=>(r)=>r))(p))))(((l)=>(r)=>(f)=>f(l)(r))((p)=>(n)=>n)((p)=>(n)=>n))))(m))(m)(n))(n)(((n)=>(p)=>(x)=>p(n(p)(x)))(c))(x))(c))(m)(n)((p)=>(n)=>n))(p =>n=>p(p(p(p(p(p(p(n))))))))(p=>n=>p(p(p(n))))))

今回はここまで

今回は基礎的な演算と再帰の仕組みを作りました。 次回はリスト構造（配列）と NIL、REDUCE、MAPを定義します。