HapInSアドベントカレンダー2024、23日目! いつも言語のことを考えているh_shimakawaです。
今回は約1年越しの超大作、ラムダ計算シリーズの最終回です。 単純なラムダ関数を組み合わせて「チューリング完全」の力を実装する、感動のお話です!
はじめに
目標
この記事では、チューリングマシンの実装を通じて、ラムダ計算の計算能力が「チューリング完全」であることを証明します。

難易度
難易度: ある程度抽象度が上がってきたのでむしろわかりやすいのかも?
対象読者
ラムダ計算やチューリング等価について関心がある人、またはない人
目次
過去記事へのリンク
ラムダ計算の記事としては1年ぶりの記事になります。 内容を忘れてしまった人は過去の記事を参照してください。
今回のテーマ ラムダ計算の計算力を確認する
今回はラムダ計算がチューリング完全であることを確認するため「チューリングマシン」を実装します。 「チューリング完全」とは大まかに「任意の計算可能な問題を解く能力を持つ」ということです。一般的なプログラミング言語、例えばJavaやPythonなどと同等の計算能力があることが証明されます。
今回はチューリングマシンの1実装であるBrainf*ck(以下BFという。)を実装します。
真偽値や数値、文字列、配列などがなく、「関数」しかない世界で組み上げられたラムダ計算が、すべてのコンピュータと同等の計算能力があるだなんて、素敵なことだと思いませんか?ワクワクしますね!
詳しくはWikipediaの記事を参照してください。
チューリングマシンとは
チューリングマシンは、アラン・チューリングが考案した計算モデルで、現代のコンピュータの基礎となる概念です。
チューリングマシンは以下の要素でできています。
- 無限に長いテープ:記号を読み書きするための媒体。
- ヘッド:テープ上を左右に移動し、記号を読み書きします。
- 状態遷移表:ヘッドの現在位置と状態に基づいて次の動作を決定します。
単純な要素の組み合わせでできた、任意の計算可能な問題を解く能力を持つことが証明されています。
詳しくはWikipediaの記事を参照してください。
BFとは
チューリングマシンを忠実に実装したプログラミング言語です。 最もコンパイラが小さくなるように設計され、”+-<>,.[]”の8個の記号で構成されたシンプルな言語です。 シンプルであるがゆえにチューリング完全を証明するためによく使われる言語です。
BFの命令は以下のようになっています。
| 命令 | 意味 | 擬似コード |
|---|---|---|
| + | 現在のセルの値を1増やす | mem[p] += 1 |
| - | 現在のセルの値を1減らす | mem[p] -= 1 |
| < | ポインタを1つ左に移動 | p -= 1 |
| > | ポインタを1つ右に移動 | p += 1 |
| , | 現在のセルに入力値を格納 | mem[p] = input() |
| . | 現在のセルの値を出力 | print(mem[p]) |
| [ | 現在のセルの値が0なら対応する]へジャンプ | while (mem[p] != 0) { |
| ] | [に戻る | } |
BFのプログラム例
10*10を計算し、100に対応する文字"d"を表示するプログラム
++++++++++[->++++++++++<]>.
詳しくはWikipediaの記事を参照してください。
チューリングマシンの実装
テープを実現する
記号の書かれたテープは、配列とみなせるのでとりあえず第3回で作成したリスト構造を使えば実現できそうですね
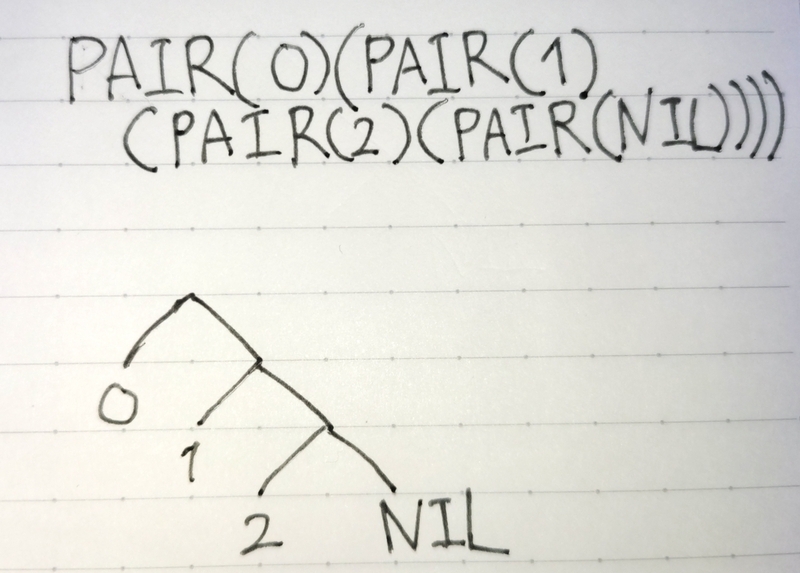
「左右に移動する」を実現する(BFの<>を実現する)
テープを左右に移動するにはどうしたらいいのでしょうか? 技術的なことを言うと、リスト構造はネストの深い方向にしか進むことができません。どうすればいいでしょうか?
好きなだけ進んで戻れる仕組みって何があるでしょうか? 例えば「ブラウザの次へ・前へ」、「Undo・Redo」ですね。 これらはスタックを2つ持つことで実現できます。
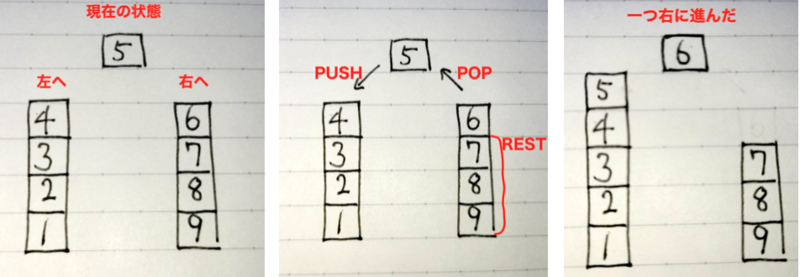
リスト構造は、一番上の値を簡単に操作できる構造なので余裕でできますね。 既存関数のPAIR/RIGHT/LEFTで実現できます。
const PUSH = PAIR; const POP = LEFT; const REST = RIGHT; // テープの生成と操作 const NEW_TAPE = (left) => (current) => (right) => PAIR(left)(PAIR(current)(right)); const LEFT_PART = LEFT; const CURRENT = (tape) => LEFT(RIGHT(tape)); const RIGHT_PART = (tape) => RIGHT(RIGHT(tape)); // 右に進む命令 const TM_RIGHT = (tape) => NEW_TAPE( // 新しい左のテープは、"現在の値"を左のテープにpushしたもの PUSH(CURRENT(tape))(LEFT_PART(tape)) )( // 新しい"現在の値"は、右のテープからpopしたもの POP(RIGHT_PART(tape)) )( // 新しい右のテープは、一つpopした残りの部分 REST(RIGHT_PART(tape)) );
ラムダ計算では値を再代入で書き換えることができません。 新しい値(新しい関数)を作ることしかできないので、テープを新たに再構成しています。
"無限に長い"テープを実現する
ここまでは順調にテープを実装できそうな感じでしたが、無限に長いテープとはどうすれば実現できるでしょうか?
リスト構造にはNILという終端が存在するので、テープの長さは無限になるはずがありません。
ここでも「ブラウザの次へ・前へ」の仕組みを参考にしてみましょう。 ブラウザでは"前へ"がない状態で新たにリンクを開いたとき、新しい履歴を作ってくれますよね? 同じやり方で作ってみましょう。
const POP_OR_ZERO = (halfTape) => IF( // テープが終端である IS_NIL(halfTape) )( // 0を返す ZERO )( // テープの残りを返す LEFT(halfTape) );
やり方は単純ですね。 終端であるNILを見つけたときに、代わりの値(ゼロ)を返すことで、テープの終端に達することなく テープの移動を続けることができます。 BFはテープがすべてゼロで初期化されていることを期待しているのでここではゼロを返しています。
トンネルを掘りながら壁を構築して進むシールドマシンみたいで格好いいですね!
テープに読み書きをする(BFの+-を実現する)
上記で作成したテープにはすでに"現在の状態"があるので、ここに存在するチャーチ数(ラムダ関数で作られた数値)を読み取って、値を増減するだけです。 これはそのままINC、DECで実現できますね。 なお、ラムダ計算はあくまでも関数ですのでリスト構造では値の書き換えができません。毎回新しいデータを生成しています。
const TM_INC = (tape) => NEW_TAPE( LEFT_PART(tape) )( INC(CURRENT(tape)) )( RIGHT_PART(tape) );
入出力について(BFの,.について)
入出力はチューリング等価であることの証明にはあまり関係しないので実装を省くことができます。 ただ、少なくとも計算結果を表示しないと何がなんだかわからないので.(文字の出力)だけ実装します。
本当は文字を出力するのですが、デバッグで使いたいので文字コードを出力しています。 明日キーコード表を脳内に展開しておいてください。 ASCIIコード表
const TM_PRINT = (tape) => { console.log(TO_INT(CURRENT(tape))); return tape; };
繰り返しについて(BFの[]の実装について)
繰り返しは再帰で実現できます。 テープの現在の値がゼロでなければ”処理”を繰り返すコードは以下のように書けます。
// 参考 const FIX = (f) => f(f); const TM_LOOP = FIX( (recur) => (list) => (tape) => (_) => IF( IS_ZERO(CURRENT(tape)) )( (_) => tape )( (_) => recur(recur)(list)(EVAL_LIST(list)(tape)(_) )(_) )(_) );
謎の引数"_"が登場しています。
これは何でしょうか。実はIFがIF(条件)(A)(B)という書き方になっているので、条件にかかわらず、引数のAB両方が評価されてしまい、無限に関数呼び出しが行われてエラーが発生します。
それを防ぐために"遅延評価"というテクニックを使用しています。 実行したい処理を関数でくるむことで、実行のタイミングを遅くすることで、IFの条件に応じた処理だけを適切に実行できます。 上記で作成したTM_{INC_DEC_RIGHT|LEFT|PRINT}関数についても呼び出し方を揃えるように、以下のように遅延評価用引数を追加します。
// 遅延評価に対応したTM_INC const TM_INC = (tape) => (_) => NEW_TAPE(LEFT_PART(tape))(INC(CURRENT(tape)))(RIGHT_PART(tape)); // 変更前の呼び出し方 TM_INC(tape) // 変更後の呼び出し方 TM_INC(tape)("not used")
命令コードの実装
前述の通りBFは+-<>,.[]の8文字でコーディングされます。 ですが、簡単のためここでは以下のように、関数を並べて記述します。
// 配列をペアリストに変換(補助関数) const toPairList = (ary) => ary.reduceRight((list, cmd) => PAIR(cmd)(list), NIL); // BFのコード // ++++++++++ // [->++++++++++<] // >. と同じ const code = toPairList([ TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_LOOP( toPairList([ TM_DEC, TM_RIGHT, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_INC, TM_LEFT, ]) ), TM_RIGHT, TM_PRINT, ]);
むしろ生のBFよりも読みやすいまでありますね! TM_LOOPについては、何を繰り返すか知る必要があるため、[]で囲まれた塊を取り込んでいます。
評価関数の作成
上記でほとんど必要な処理は完成しているので、あとは命令コードを受け取って適切な命令コードを実行する仕組みを作成します。
// BFの命令を実行 const EVAL_LIST = FIX( (recur) => (list) => (tape) => (_) => IF( // 終端かどうか IS_NIL(list) )( // 終端なら現在のテープを返却 (_) => tape )( // 終端でない時、リストの先頭を評価して、EVAL_LISTを再帰呼び出し (_) => recur(recur)(RIGHT(list))(LEFT(list)(tape)(_))(_) )(_) );
これで完成です。
実行してみましょう。
//テープの中身を表示(補助関数) const showTape = (tape) => { const left = TO_ARRAY(LEFT_PART(tape)); const current = TO_INT(CURRENT(tape)); const right = TO_ARRAY(RIGHT_PART(tape)); return left.reverse().join(',') + ',[' + current + '],' + right.join(','); }; // テープの初期化 const tape = NEW_TAPE(NIL)(ZERO)(NIL); // コードの実行 // 第3引数はダミーで評価されない const result = EVAL_LIST(code)(tape)(NIL); // => "d" console.log('tape=', showTape(result)); // => 0,[100],
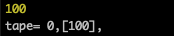
ちゃんと100("d")が出力されましたね。 補助関数も正しく動いているようです。
最後に
今回の記事ではラムダ計算にチューリング完全な計算能力があることを証明してきました。 異常なほど簡単な関数だけを組み合わせて真偽値やif、数値と四則演算、リスト構造と繰り返し処理など プログラミング言語で必要とされる基本的な機能を組み上げてきました。
一般的にコンピュータの根源とは、電子であるとかビット演算だと答える人も多いかと思うのですが 今回の記事で取り上げたラムダ計算は「計算の根源」であり、 それが実際に計算能力があることを証明できるところまで計算の体系を構築することは、 とてもエキサイティングな体験でした。
実際のところラムダ計算がチューリング完全であることは調べれば簡単にわかることであって、 わざわざチューリングマシンを実装する必要なんてどこにもありません。
しかし、言葉で理解するだけではなく、実際に手を動かして構築し証明することで、 具体的な自身の体験として紐づくことから深い理解が得られたと思います。
皆さんもいい経験になると思いますので、試してみてはいかがでしょうか?
全てのソースコードは以下に公開してありますので、 わからなくなった時に使ってみてください。
https://github.com/hoznas/lambda-calculus
展開
const result=((f)=>f(f))((recur)=>(list)=>(tape)=>(_)=>((c)=>(x)=>(y)=>c(x)(y))(((x)=>x((a)=>(b)=>(c)=>(x)=>(y)=>y)((x)=>(y)=>x))(list))((_)=>tape)((_)=>recur(recur)(((p)=>p((l)=>(r)=>r))(list))(((p)=>p((l)=>(r)=>l))(list)(tape)(_))(_))(_))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))(((f)=>f(f))((recur)=>(list)=>(tape)=>(_)=>((c)=>(x)=>(y)=>c(x)(y))(((n)=>n((x)=>(x)=>(y)=>y)((x)=>(y)=>x))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))((_)=>tape)((_)=>recur(recur)(list)(((f)=>f(f))((recur)=>(list)=>(tape)=>(_)=>((c)=>(x)=>(y)=>c(x)(y))(((x)=>x((a)=>(b)=>(c)=>(x)=>(y)=>y)((x)=>(y)=>x))(list))((_)=>tape)((_)=>recur(recur)(((p)=>p((l)=>(r)=>r))(list))(((p)=>p((l)=>(r)=>l))(list)(tape)(_))(_))(_))(list)(tape)(_))(_))(_))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>((p)=>p((l)=>(r)=>l))(n((p)=>((l)=>(r)=>(f)=>f(l)(r))(((p)=>p((l)=>(r)=>r))(p))(((n)=>(p)=>(x)=>p(n(p)(x)))(((p)=>p((l)=>(r)=>r))(p))))(((l)=>(r)=>(f)=>f(l)(r))((p)=>(n)=>n)((p)=>(n)=>n))))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((l)=>(r)=>(f)=>f(l)(r))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape))(((p)=>p((l)=>(r)=>l))(tape)))(((halfTape)=>((c)=>(x)=>(y)=>c(x)(y))(((x)=>x((a)=>(b)=>(c)=>(x)=>(y)=>y)((x)=>(y)=>x))(halfTape))((p)=>(n)=>n)(((p)=>p((l)=>(r)=>l))(halfTape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((p)=>p((l)=>(r)=>r))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape))))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>l))(tape))(((n)=>(p)=>(x)=>p(n(p)(x)))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>l))(tape)))(((halfTape)=>((c)=>(x)=>(y)=>c(x)(y))(((x)=>x((a)=>(b)=>(c)=>(x)=>(y)=>y)((x)=>(y)=>x))(halfTape))((p)=>(n)=>n)(((p)=>p((l)=>(r)=>l))(halfTape)))(((p)=>p((l)=>(r)=>l))(tape)))(((l)=>(r)=>(f)=>f(l)(r))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape))))((x)=>(y)=>y)))))))))))))))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))(((l)=>(r)=>(f)=>f(l)(r))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape))(((p)=>p((l)=>(r)=>l))(tape)))(((halfTape)=>((c)=>(x)=>(y)=>c(x)(y))(((x)=>x((a)=>(b)=>(c)=>(x)=>(y)=>y)((x)=>(y)=>x))(halfTape))((p)=>(n)=>n)(((p)=>p((l)=>(r)=>l))(halfTape)))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape)))(((p)=>p((l)=>(r)=>r))(((tape)=>((p)=>p((l)=>(r)=>r))(((p)=>p((l)=>(r)=>r))(tape)))(tape))))(((l)=>(r)=>(f)=>f(l)(r))((tape)=>(_)=>{console.log(((x)=>x((n)=>n+1)(0))(((tape)=>((p)=>p((l)=>(r)=>l))(((p)=>p((l)=>(r)=>r))(tape)))(tape)));return tape;})((x)=>(y)=>y))))))))))))))(((left)=>(current)=>(right)=>((l)=>(r)=>(f)=>f(l)(r))(left)(((l)=>(r)=>(f)=>f(l)(r))(current)(right)))((x)=>(y)=>y)((p)=>(n)=>n)((x)=>(y)=>y))((x)=>(y)=>y);